Télécharger cette fiche conseil au format PDF
Pourquoi utiliser les probabilités dans une étude marketing ?
Par exemple, lors d’un test de produit, on obtient les résultats suivants : 55 % des personnes interrogées préfèrent le produit A et 45 % préfèrent le produit B.
Le résultat est-il une conséquence du hasard ?
Si l’on refait le test, obtient-on un résultat similaire ?
A est-il préféré à B ?
Les risques :
1. Risque α : Risque de croire vraie une différence qui n’existe pas
2. Risque β : Risque de ne pas voir une différence qui existe en réalité
MOYENNE ET ECART-TYPE
- Moyenne : valeur moyenne d’une réponse (pour les réponses sur une échelle).
- Ecart-type : mesure la dispersion d’une variable.
A noter également :
- Médiane : valeur telle que 50 % des réponses sont supérieures et 50 % sont inférieures,
- Mode : réponse le plus souvent donnée (par exemple quand on demande un prix estimé).
LA NOTION D’INTERVALLE DE CONFIANCE
Soit m le résultat d’un sondage, la mesure approximative de la valeur réelle inconnue est M.
L’intervalle de confiance permet de délimiter la zone où se trouve la valeur réelle.
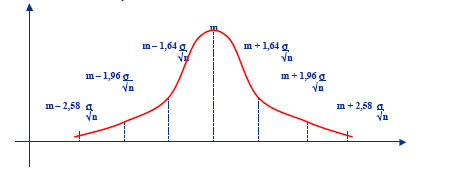
QUELQUES PRINCIPES DE BASE
- La précision d’une mesure dépend de la dispersion de la variable (moins une variable est dispersée, meilleure est la précision)
- La précision d’une mesure croît avec la taille de l’échantillon (exactement avec la racine carrée de la taille de l’échantillon)
Donc améliorer la précision coûte de plus en plus cher - La précision d’une mesure ne dépend pas du taux de sondage (1 personne sur 1 000 ou 1 personne sur 1 000 000)
Conséquence : La taille de l’échantillon est indépendante de la taille de la population
Exemple : afin d’atteindre un même niveau de précision, il faut prendre la même taille d’échantillon pour l’élection présidentielle et pour chaque élection municipale
LA NOTION DE SEUIL DE SIGNIFICATIVITE
Dire qu’une différence est significative à .10 (ou 10%) signifie : il y a 90% de chances que la différence ne soit pas due au hasard
De même :
- 0.5 (ou 5%) signifie : il y a 95% de chances que la différence ne soit pas due au hasard
- 0.1 (ou 1%) signifie : il y a 99% de chances que la différence ne soit pas due au hasard
Habituellement, on demande à l’institut d’indiquer les différences significatives à partir d’un risque de 10 % (avec le plus souvent une notation spécifique des différences significatives à 5% et 1%)
LES 3 PRINCIPALES FAMILLES DE TESTS STATISTIQUES
TEST DU CHI 2 (comparaison de tableaux de pourcentages -croisement de 2 variables-)
Le test du c2 (prononcez khi deux ou khi carré) fournit une méthode pour déterminer la nature d’une répartition, qui peut être continue ou discrète. Nous nous occuperons ici de déterminer si une répartition est uniforme dans le cas discret.
- Méthode
On répartit les valeurs de l’échantillon (de taille n) dans k classes distinctes et on calcule les effectifs de ces classes.
Appelons oi (i=1,…,k) les effectifs observés et ei les effectifs théoriques.
On calcule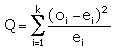
La statistique Q donne une mesure de l’écart existant entre les effectifs théoriques attendus et ceux observés dans l’échantillon. En effet, plus Q sera grand, plus le désaccord sera important. La coïncidence sera parfaite si Q=0.
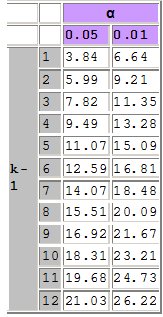
On compare ensuite cette valeur Q avec une valeur issue d’un tableau (voir extrait ci-après) à la ligne k-1 et à la colonne α..(k-1 est le nombre de degrés de liberté et α la tolérance.)
Si Q > 
, et si n est suffisamment grand, alors l’hypothèse d’avoir effectivement affaire à la répartition théorique voulue est à rejeter avec une probabilité d’erreur d’au plus α..
- Exemple
On a lancé un dé 90 fois et on a obtenu les issues 1 à 6 (k=6) avec les effectifs suivants: 12, 16, 20, 11, 13, 18. Si le dé n’est pas pipé (notre hypothèse), on attend comme effectifs moyens théoriques 15 pour toutes les issues.
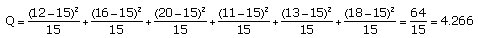
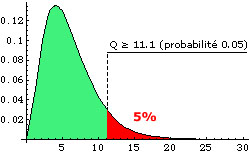
Pour k-1=5 degrés de liberté et un seuil de tolérance de 5%, la valeur du tableau est 11.1. Cela signifie que la probabilité que Q soit supérieur à 11.1 est de 5% (voir figure ci-dessous). Comme 4.266 < 11.1, on accepte l’hypothèse selon laquelle le dé est régulier.
TEST DU T DE STUDENT
Le test de Student est un test de significativité qui peut être employé :
- lors de la comparaison de deux moyennes (ce test ne peut être utilisé qu’à deux conditions : les distributions des moyennes sont normales, c’est-à-dire décrivent une courbe de Gauss, et leurs variances sont de même taille)
- pour tester la significativité d’un coefficient de régression
En ce qui concerne la comparaison de deux moyennes, on se pose la question suivante : On se pose la question suivante : la différence entre la moyenne observée et la moyenne de la population est-elle significative ou non ?
Le test t de Student permet de répondre à ce genre de question. Le test t est calculé en effectuant le rapport de la différence des moyennes sur l’erreur standard et on obtient alors une valeur appelée « Valeur de t » ou t observée).
Après avoir effectué le test de significativité globale du modèle de régression multiple (test de Fisher), il est intéressant d’effectuer un test de significativité partielle sur le même modèle à l’aide du test de Student. Ce test nous permettra de savoir si chaque coefficient est significativement différent de 0 ou non et ainsi de savoir si telle variable explique réellement la variable Y.
- Principe d’utilisation :
La valeur observée est comparée aux valeurs contenues dans la table du t de Student. La table du t de Student permet de déterminer pour la valeur observée (en fonction du nombre de degrés de liberté correspondant le seuil de probabilité auquel correspond le t observé. Si la valeur absolue du t calculé est supérieure à la valeur du t de la table de Student, on en concluera soit que la différence est significative, soit que le coefficient est significativement différent de 0, selon l’emploi du test de Student. On considère communément qu’une valeur de t correspondant à un seuil p
TEST DU F DE FISCHER (ANALYSE DE VARIANCE)
Le test F de Fisher est un test de significativité qui peut être employé :
– lors de la comparaison de plusieurs moyennes (ce test ne peut être utilisé qu’à deux conditions: les distributions des moyennes sont normales, c’est-à-dire décrivent une courbe de Gauss et leurs variances sont de même taille)
– pour tester la significativité globale d’un modèle de régression
En ce qui concerne la comparaison de plusieurs moyennes, on se pose la question suivante : les différences entre les moyennes observées et la moyenne globale sont-elles significatives ou non ?
Le test F de Fisher permet de tester ce genre d’hypothèses.
Le test de Fisher permet également de savoir si un modèle de régression linéaire multiple est globalement significatif ou non.
- Principe d’utilisation :
La valeur observée est comparée aux valeurs contenues dans la table du F de Fisher. Si la valeur du F calculé est supérieure à la valeur du F critique de la table, alors on en déduira qu’un ou plusieurs coefficients de la régression sont différents de 0, et donc que le modèle est (très) significatif (selon le seuil de significativité). Si le modèle n’est pas globalement significatif, il est important de voir quel(s) coefficient(s) n’est pas significatif(s) à l’aide du test de Student. Un F calculé supérieur au F de la table traduit, soit une différence significative entre les moyennes observées et la moyenne globale, soit un modèle globalement significatif, selon l’emploi du test de Fisher.