Echantillonnage

• Principe
  Il consiste à choisir des individus de telle sorte que chaque membre de la population a une chance égale de figurer dans l’échantillon. Ce choix peut se faire avec remise ou sans remise : avec remise, un individu peut être choisi plusieurs fois ; sans remise, un individu déjà choisi ne peut l’être de nouveau. C’est le cas habituel.
• Méthode
  Numéroter tous les individus de la liste correspondant aux individus de la population avec des nombres comportant un même nombre de chiffres. Puis utiliser une table de nombres aléatoires, une calculatrice ou un programme informatique, pour obtenir des nombres aléatoires comportant le nombre de chiffres désiré.Enfin, sélectionner les nombres qui coïncident avec la liste. On rejette les nombres qui ne coïncident pas avec la liste ou qui se répètent, on s’arrête après avoir sélectionné n individus (n représentant le nombre d’individus souhaités dans l’échantillon).
  Avec Excel

  • Première colonne : identifie avec un nombre chaque individu de la liste de référence.
  • Deuxième colonne : =alea()
  • Recopier les deux colonnes en valeur à la même place.
  • Trier les deux colonnes en fonction de l’ordre croissant (ou décroissant) de la deuxième colonne.
  • Retenir les n premiers individus dans la colonne 1

  Combien peut-on réaliser d’échantillons ?
  Si l’on note n la taille de l’échantillon et N la taille de la population.
  

  Avec remise :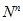
  Sans remise :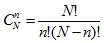

   

• Avantage de cette méthode : On peut espérer un échantillon « représentatif » puisque la méthode donne à chaque individu de la population une chance égale.
• Inconvénients : la méthode n’est applicable que lorsqu’il existe une liste exhaustive de toute la population.

• Principe
  L’échantillonnage systématique est une méthode qui exige aussi l’existence d’une liste de la population où chaque individu est numéroté de 1 jusqu’à N.
  Notons n, le nombre d’individus que doit comporter l’échantillon (la taille de l’échantillon). L’entier voisin de N/n sera noté « r » et appelé « raison » de sondage ou « pas » de sondage.
• Méthode
  Choisir au hasard un entier naturel d entre 1 et r (cet entier sera le point de départ). L’individu dont le numéro correspond à d est le premier individu.Pour sélectionner les autres, il suffit d’ajouter à d la raison de sondage : les individus choisis seront alors ceux dont les numéros correspondent à
  d + r
  d + 2r
  d + 3r
  etc…
• Avantages: facile à sélectionner parce qu’un seul individu est choisi au hasard.On peut obtenir une bonne précision parce que la méthode permet de répartir l’échantillon dans l’ensemble de la liste.
• Inconvénients : Les données peuvent être biaisées à cause de la périodicité.
• Exemple
  Etude des déplacements en autobus sur 365 jours en prenant un échantillon de taille 60. (N=365 jours et n=60).
• Remarques
  On a une population de 400 individus, on veut un échantillon de 100 individus
  R = 4
  On a donc que 4 échantillons possibles
  1, 5, 9, …. 397
  2, 6, 10, … 398
  3, 7, 11, ….399
  4, 8, 12, … 400Si la population est distribuée au hasard dans la base de sondage, un échantillonnage systématique donnera des résultats similaires à ceux d’un échantillonnage aléatoire simple.
  Cette méthode est très utilisée dans les contrôles de qualité.
  L’échantillonnage avec une probabilité proportionnelle à la taille.
  Si la base de sondage renferme de l’information sur la taille de chaque unité (comme le nombre de médecins d’un hôpital) et si la taille des ces unités varie, on peut utiliser cette information pour accroître l’efficacité de l’échantillonnage.
  Plus la taille de l’unité est grande, plus sa chance d’être incluse dans l’échantillon est élevée

• Principe
  1. On subdivise la population en strates (groupes relativement homogènes) qui sont mutuellement exclusives
  2. Proportionnellement à son importance dans la population, on calcule combien il faut d’individus au sein de l’échantillon pour représenter chaque strate.
  3. Dans chacune des strates, on choisit au hasard le nombre nécessaire d’individus
  Les variables de stratification doivent être simples à utiliser, facile à observer et étroitement reliées au thème de l’enquête.
• Avantages
  Il est peu probable de choisir un échantillon absurde puisqu’on s’assure de la présence proportionnelle de tous les divers sous-groupes composant la population.
• Inconvénients
  La méthode suppose l’existence d’une liste de la population. Il faut aussi connaître comment cette population se répartit selon certaines strates.
• Exemple
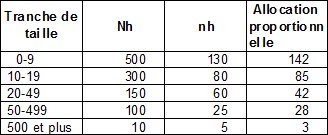
  Choisir par échantillonnage stratifié 10 élèves dans un groupe de 60, en tenant compte du fait que 50% d’entre eux sont en CP, 30% en CE1 et 20% en CE2.
  La variance totale est la somme de la variance intrastrate et de la variance interstrate.
  On cherche à avoir la plus petite variance intrastrate et une grande variance interstrate

   

• Estimation
  Echantillonnage aléatoire simple intrastrate

  Moyenne générale :	Précision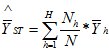
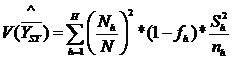
  H = Nombre de strates	fh = taux de sondage dans la strate h nh = taille de l’échantillon de la strate h S2h = dispersion vraie au sein de la strate h

• Application numérique
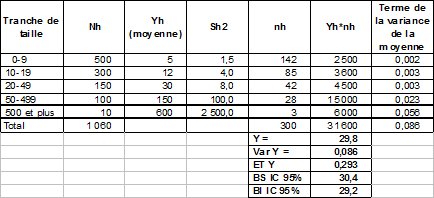
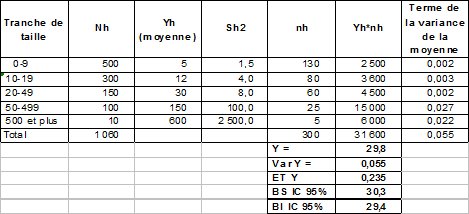
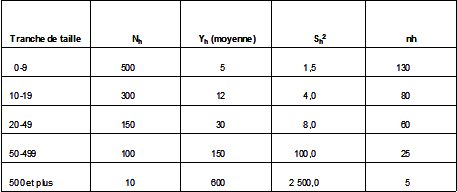  On dispose de 1060 hôpitaux. On s’intéresse au nombre moyen Y de médecins par hôpital. La population est définie par 5 strates par tranches de taille en fonction du nombre de médecins. Cette information est obtenue à partir de documents de l’APHP ne donnant pas le nombre exact de médecins mais seulement la tranche de taille. Réalisant un sondage aléatoire simple dans chaque strate h selon un budget permettant d’enquêter globalement 300 hôpitaux, on mesure yh et la dispersion Sh2 de la variable nombre de médecins dans l’échantillon des hôpitaux tirés. Les allocations par strates sont données dans la dernière colonne du tableau.Quel est l’estimateur de Y, et quelle est sa précision ?
  

  Quelle serait l’allocation proportionnelle ?
  

  

• Principe
  Dans les méthodes précédentes, l’unité statistique était choisie individuellement.
  La technique de l’échantillonnage en grappes entraîne la division de la population en groupes ou grappes.
  On sélectionne au hasard un certain nombre de grappes (unités primaires) pour représenter la population. Puis on sélectionne tous les individus des grappes choisies. 
• Avantages
  La méthode ne nécessite pas une liste globale de la population puisque seules les individus inclus dans les grappes comptent. Elle permet de limiter l’échantillon à des groupes compacts ce qui permet de réduire les coûts de déplacement, de suivi et de supervision.
• Inconvénients
  La méthode peut entraîner des résultats imprécis (moins précis que les méthodes précédentes) puisque les unités voisines ont tendance à se ressembler. Elle ne permet pas de contrôler la taille finale de l’échantillon.

• Principe
  Ressemble à l’échantillonnage en grappes, sauf que dans ce cas on prélève un échantillon à l’intérieur de chaque grappe.
  Ce qui implique au moins deux degrés (mais cela peut être plus) d’échantillonnage : on identifie au premier degré les grandes grappes (unités primaires), puis au second degré, à l’intérieur de chaque grappe, on sélectionne les unités (unités secondaires) qui vont faire partie de l’échantillon.
• Avantages
  L’échantillon est plus concentré ce qui réduit les coûts, pas besoin de disposer de la liste de toutes les unités. La méthode permet de contrôler la taille de l’échantillon notamment par stratification.
• Inconvénients : précision des résultats, taille plus grande que dans le cas d’un échantillonnage aléatoire simple.

• Principe
  Les données de base sont collectées auprès d’un échantillon d’unité de grande taille, ensuite pour un sous-échantillon de ces unités, la collecte des données est plus détaillée.
  Le plus couramment on utilise deux phases ou échantillonnage double. A première phase consiste donc à « filtrer » le premier échantillon par le biais d’un questionnaire par exemple.
  L’échantillonnage à plusieurs phases est assez différent de l’échantillonnage à plusieurs degrés, malgré les similarités entre eux sur le plan de leur appellation.
  L’échantillonnage à plusieurs phases est utile lorsqu’il manque à l’intérieur de la base de sondage des données auxiliaires qui pourraient servir à stratifier la population ou à rejeter à la sélection une partie de la population et lorsqu’on dispose d’un budget insuffisant pour recueillir des données auprès de l’échantillon entier (ou lorsque recueillir des données auprès de l’échantillon entier imposerait un fardeau excessif aux répondants).

Méthodes non aléatoires

On oppose aux méthodes aléatoires les méthodes non aléatoires ou empiriques.
Dans le cas de l’échantillonnage probabiliste, chaque unité a une chance d’être sélectionnée. Dans celui de l’échantillonnage non probabiliste, on suppose que la distribution des caractéristiques à l’intérieur de la population est égale. C’est ce qui fait que le chercheur croit que n’importe quel échantillon serait représentatif et que les résultats, par conséquent, seront exacts. Pour l’échantillonnage probabiliste, la randomisation est une caractéristique du processus de sélection, plutôt qu’une hypothèse au sujet de la structure de la population.
Dans le cas de l’échantillonnage non probabiliste, puisqu’on choisit arbitrairement des unités, il n’existe aucune façon d’estimer la probabilité pour une unité quelconque d’être incluse dans l’échantillon. Également, comme la méthode en question ne fournit aucunement l’assurance que chaque unité aura une chance d’être incluse dans l’échantillon, on ne peut estimer la variabilité de l’échantillonnage ni identifier le biais possible.
On ne peut mesurer la fiabilité d’un échantillonnage non probabiliste; la seule façon de mesurer la qualité des données en résultant consiste à comparer certains des résultats de l’enquête à l’information dont on dispose au sujet de la population. Encore une fois, rien ne fournit l’assurance que les estimations ne dépasseront pas un niveau acceptable d’erreur. Les statisticiens hésitent à utiliser les méthodes d’échantillonnage non probabiliste, parce qu’il n’existe aucun moyen de mesurer la précision des échantillons en découlant.
Elles sont souvent utilisées

• pour des études exploratoires;
• pour réduire les coûts;
• quand il est impossible ou non envisageable d’utiliser la méthode aléatoire.